飛行機の飛ぶ訳(流体力学の話)

早川尚男（京都大学大学院人間・環境学研究科）

(物理学概論第N回)

私が幼い頃はまだ飛行機に乗る事自体が珍しくて、乗った事がある子供はその事を自慢したりしたものである。しかし現在では国内でもちょっとした遠距離の移動には飛行機が日常的に使われる様になっており、そんな子供の自慢そのものも成り立たなくなっているのであろう。飛行機の急速な普及は飛行機の発明自体が20世紀の産物であることを考えると驚くべきものがある。では何故飛行機が飛ぶのかを簡単に答えられるのかと云えば、それほど易しくはない。きっちりとした説明を求めるのであれば流体力学を本格的に勉強する必要がある。
しかしこの問を理論物理を研究している大学院生に聞いてみても殆んどはかばかしい答えが帰って来ない。そもそも理論物理の教程では流体力学は軽んじられており、また研究対象が日常生活と解離している場合にはそういった疑問も持たないのであろう。従って諸君が「鉄の塊が飛ぶのを信じない」という態度を取ったとしても余り責める事はできない。

この問は自然と思い付くものであるから、日常の科学に答える様な本等にも取り上げられている。そこでの解答はの定理によるというものである。平たく云ってしまえばベルヌーイの定理(もうちょっと詳しい説明。)とは流れに沿って圧力 \(P\) と運動エネルギー(密度) \(ρv^2/2\) と位置エネルギー(密度)の和が一定に保たれるというものである。重力 \(g\) の下の条件ではポテンシャル(密度)は \(ρg z\) になるのでベルヌーイの定理を式で書けば

\[
P+ρv^2/2+ρg z=一定
\]

となる。ここで \(ρ\) は質量密度、 \(z\) は高さである。一見圧力がエネルギー(密度)と並列で現われるのは奇異に映るが、静水圧はポテンシャルと同様に深さと単位体積辺りの質量に比例することを考えると、ポテンシャルと圧力は同等の役割を果たす。またやや詳しい導出の説明を見れば分かる通り、ベルヌーイの定理は粘り気の全くないと仮定した理想的な流体(粘性の働かない完全流体)のエネルギーの保存を表している。

さて一見もっともな飛行機が飛ぶ理由の説明は次の様なものである。翼がやや水平から上向きに傾いているとしよう。翼の上面で空気は大きく迂回する必要があるが下面ではその必要はない。翼に隔てられた空気は再び合流するが、そこで上方と下方で空気移動の所要時間に差があると定常の流れになりそうもないので上の方では流れが速くなるだろう。(ポテンシャルの影響は無視できるほど翼は薄いので)ベルヌーイの定理から翼の上方では圧力が低く、圧力差によって揚力が生じるというものである

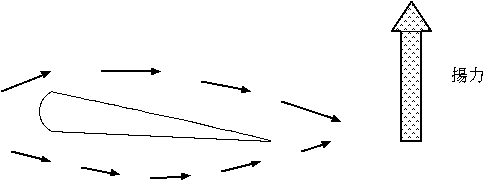
実は同時到着の仮定は間違っている。実験ではそれよりも翼の上面で高速になることが分かっている。しかしその事は上の説明を補強こそすれ、否定的な意見とはならない。従って、ベルヌーイの定理に基づく説明が全く間違っている事にはならない。航空工学の出身の人(或は物理出身でも流体力学をしっかり身につけている人)はこう付け加えるのではないであろうか。循環(渦を足し合わせたものと同じだと思って下さい。或は巨視的な渦)が必要である。時計回りの循環があれば例え円柱の様な対称な形状のものでも、左から来た流れに対しては上方で加速されるし、下方では減速される。循環は流れが曲率を持っている、即ちマクロに曲がっていれば必ず存在する。こうした循環があれば、流体からエネルギーを貰って、いかにも揚力が働きそうである(図では上向き)。実際、流体粒子が曲線運動をする際には曲率中心に向かって求心力が必要である。そうでなければ粒子がカーブできないのは力学が教える所である。しかしこの場合、重力は殆んど効かないし、誰かが曲率(回転)中心から引っ張っている訳ではない。そう考えると求心力をまかなうのには圧力しかありえない。圧力がバランスしていると力が働かないので実際には圧力勾配が求心力となっており、その大きさは曲率(回転)半径に反比例する事が知られている。そう考えると翼の上面で圧力がより低下しており上に上に翼が押し上げられると理解でき、またベルヌーイの定理から流速が速い事も分かる。また揚力を具体的に計算するためにはクッタ・ジューコウスキーの定理というのがあって、速度と循環に比例する揚力が働くという事を教えてくれるであろう。

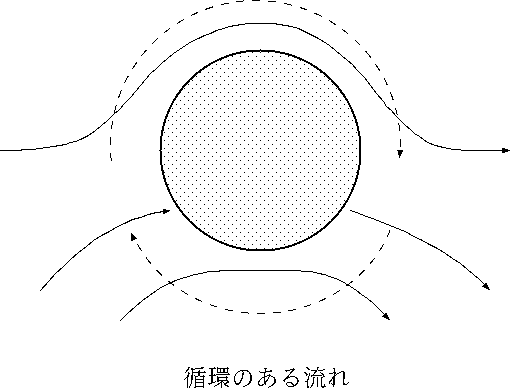
いささか脱線するが図2を見て思い出すものはないだろうか。野球のボールと見えないだろうか。カーブがどうして曲がるのかという説明にはここでの説明がそのまま使える。本にはマグヌス力によると書いてあるかもしれないが、そんな用語は不要である。この図に描いた循環はカーブを投げるときのひねりである。カーブ回転を与えたらボールがカーブすることは実際に手を動かしてみればいい。縦に落ちるカーブ(昔はドロップと云った)も同じ原理で曲がる。

こうして大団円になりそうだが、しかしここで問題が生じる。循環(渦)が揚力を生じさせると云っても都合良く時計回りの循環が生じる必然はないのではないか?或はそもそもベルヌーイの定理を使っていいのか、という疑問が湧く。実際、ベルヌーイの定理の成立のために仮定されたのは粘性を無視した理想的な流体の存在であり、実際にはそんな物質はあり得ないからである。実際、そのことを真面目に考えると深刻な問題に直面する。
完全流体では粘性がないから力学の保存則に対応するものが成立する。質量の保存は流量の保存、運動量の保存は流体の運動方程式、エネルギーの保存はベルヌーイの定理である。そんな中で角運動量の保存則に対応するものが渦度、或は循環の保存になる。従って完全流体では循環は不生、不滅であるという定理があり、そもそも循環なんか生じないのである。この矛盾をつくと流体力学をある程度勉強した学生もここで答えに窮する場合が多いだろう。今までの説明は全く解答となっていないのであろうか。

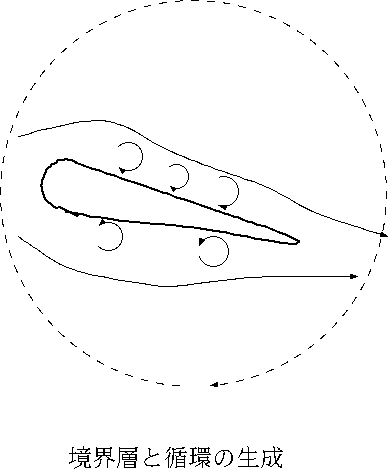
正しい解答は(1)空気が完全流体であるという仮定が間違っており、境界層と呼ばれる薄い領域で粘性の影響があって、そこで渦の発生、ひいては循環の発生がある.(2)しかし境界層を離れるとほぼ完全流体として考えてよく今までの説明に本質的な間違いはない,というものである。実際には空気には僅かに粘性があって、物体との境界では相対速度は0になる。(完全流体ではその制約はなく、接線方向には大きな値で流れている)。飛行機の様に高速で飛ぶ場合には境界層と呼ばれる非常に薄い領域で接線方向には相対速度0からほぼ飛行速度まで遷移する。その様な強いずり(せん断)がかかった状態では次々と小さな渦が生じてちょうど車輪が転がる様な状態になっている。この渦による車輪を力学的な存在と考えれば転がる事で力を翼に及ぼす。翼の斜め下から流れがあたった状態ではほぼ完全流体に対する説明のときと同様に上方で流体粒子が回り込もうとし、圧力差が生じ、上面では速い流速を得る。従ってより強いずりが翼の上面でかかる。上方で速度が速いとするとより強いずりがかかって全体として時計回りの渦が沢山生じ、時計回りの循環になる。(巨視的な渦が循環であったことを思い出そう。)循環が生じた後の揚力発生のメカニズムは既に述べたものの繰り返しである。このようにして飛行機が飛ぶ事ができるのである。(ちなみに翼からかなり離れた後方で翼に生じた循環を打ち消す逆向きの循環が生じる)。

揚力の考え方に馴染んでからスキーのジャンプを見ると興味が増すのではないであろうか。何故向かい風の場合の方が飛距離が出るのかという事に疑問を持った事のある人は多いかもしれないが、向かい風であれば相対速度が増して揚力が大きくなるからである。残念乍ら流体力学で揚力を論じるときは2次元であることを仮定しているので最近のスキーを広げたV字の様に断面積を大きくして揚力を大きくしようという素朴な発想は科学者からは出なかった様である。しかし奥行きを考えて翼やジャンプする人も何もなければ循環の生じる余地がない事を考えれば断面積の大きい方が揚力が大きい事は合点がいくであろう。

一方、ゴルフや野球のボールは追い風の方がよく飛ぶ。これは今までの説明に反しているのではなかろうか。これらのボールは図2を見れば分かる通り、速度が上面で極端に速度が増加する訳ではない。また投手が投げた程度の速度やゴルフの打ち出された速度程度では飛翔を維持できるほど揚力の効果は大きくなく、せいぜい曲がるとかちょっと浮かぶ、沈むといった効果程度しか期待できない。一方で形状から粘性から生じる抵抗が無視できない程大きくなる。従って、これらの問題では初速で与えられた運動エネルギーをどう保つかという事に帰着するからである。勿論相対速度が大きい程抵抗が大きく、エネルギーの減衰が激しい。従って追い風の方がよく飛ぶ事になる。
さて蛇足ではあるが、揚力の応用例として次の様な事を考えてみよう。ピンポン玉を2個糸で吊してその間に息を吹きかけるとどうなるか。もうここまで来たら読者諸君は答えは分かっていると思う。上図のように循環はピンポン玉の左右に互いに反対に生じ、その結果として両者はひっつこうとする。一方、雨粒等はゆっくりと落ちて来るときに互いを避けようとする(下図)。これは粘性の力が支配的となって、物体の影響で流線がゆがみ(絵が歪んでいるのは下手糞だからである)、その結果として互いを押し合うのである。実は紙をゆっくりと床に落したときに床の上を滑べるように動く事もこうした粘性の影響である。実はこうした粘性をまともに考えると、図にある様な2つの玉は決して衝突することは出来ない。では空気中で玉同士が衝突するのは何故か?実はそれは流体力学の枠の中では答えられない難しい問題であって、現在も研究がなされている。ここで少し触れた粘性の影響やそれが支配的である場合、流体のその他の話題は次回で改めて説明する事にしよう。

1. ライト兄弟が初飛行に成功したのは1903年。
2. もっともジャンボが周航して、コンコルドが完成した30年程 前からは殆んど何も変わっていない気もする。
3. 例えば：佐伯平二、はてなぜどうしてガリレオクイ ズ(合同出版、1997)
4. Daniel Bernoulli (1700-1782) オランダの物理学者、 数学者。
5. ここでの説明は今井功、パラドックスの効用、続物理の 散歩道(岩波, 1964)に準拠。